Le Docteur Faustroll aurait, au XIXème siècle, calculé la surface de Dieu !
Ce savant pataphysicien tout droit sorti de l'imagination d'Alfred Jarry conclura que « Dieu est le point tangent de zéro et de l'infini. »
Des recherches sur le sujet ont également été effectuées par Boris Vian et René Daumal.
Wikipedia.org – Surface de Dieu
Wikipedia.org – Docteur Faustroll
il devait s'ennuyer le pauvre homme. Pour penser à un truc aussi loufoque….
ça me rappel quand on m'a demandé de prouver que 637 était divisible par 5.
A défaut d'avoir découvert la surface de dieu, j'aurai découvert la pataphysique. C'est la science qui a permis de calculer la fameuse surface.
De ce que j'ai compris, la pataphysique se base sur des approximations. Ainsi, partant du principe que :
0 = 0.00001
et que
0.00001 = 0.00002
et que… et que
0.00009 = 1
on peut démontrer que 0 = 1.
Vérification : On multiplie les deux membres de l'égalité par l'infini :
0 * l'infini = 1 * l'infini
l'infini = l'infini.
Donc 0 = 1
CQNFPD
Du coup avec leur science à deux francs on peut démontrer tout ce qu'on veut. La surface de Dieu, le volume d'un de ses pets, la surface d'un point, le nombre de fois que Chuck Norris à compter jusqu'à l'infini, combien fait 7 divisé par 0, ...
Ce qui est grave c'est qu'après que le collège de pataphysique ait fermé en 1975, il a rouvert en 2000. Ils avaient du faire une faute de calcul pour la fin du monde.
@Loof : oui mais l'intellectuel, quand il se lève, va dans la bonne direction, lui.
@ Voan: D'où tiens tu que 0*infini = infini ? Tu aurais du plutôt prendre un exemple où 1 = 2 car la ta “démonstration” regrettablement approximative aurait eu un semblant de soupçon de véracité
Il a tous simplement dit que on prend comme hypothèse que 0=0,00001, or 0,00001*infini sera égale a l'infini…
@Voan & Thib:
Non, 0 n'est pas égal à 0.00001, mais à 0,(0)1
-> http://www.spontex.org/le_saviez_vous/524/
Par ailleurs, 0* infini= 0 quand tu prends le vrai 0, la démonstration manque de base solide.
Pour montrer que 1=0, voici comment s'y prendre:
tu prends 2 nombres a et b, avec a=b!=0 (!= signifie différent)
comme a=b, on a
a²=b²=ab, c'est élémentaire
donc
a²-b²=a²-ab, rien de plus difficile ici,
par conséquent, en factorisant,
(a+b)(a-b)=a(a-b), vous suivez toujours?
on simplifie simplement par (a-b), on trouve
a+b=a,
d'où
b=0
par conséquent,
1=b/b=0
1=0 CQFD (ou pas)
La pataphysique a encore gagné…
simplifie simplement par (a-b) , on trouve (...) 1=0
Oui, c'est pour cela que “simplifier” par 0 n'est pas possible. Je ne suis pas fan de ce genre de démonstration à la con. Cela revient à faire semblant de ne pas connaître ses tables de multiplication et écrire 8×7=58. C'est faux, ça ne présente pas plus d'intérêt, simplement l'erreur est moins flagrante pour un mec n'ayant pas trop fait de maths.
Par ailleurs, 0* infini= 0 quand tu prends le vrai 0
Non. 0* l'infini est une forme indéterminée en prenant le langage mathématique du lycée. En pratique, ce type d'équation ne veut pas dire grand chose, on aboutit à ce type de chose lorsque l'on calcule des limites, et il est alors possible de calculer des équivalents qui nous renseignent sur la valeur de ce produit.
Mais ce n'est pas ce qu'ils ont dit. Ils ont simplement signifié que dès lors qu'un nombre n'est pas rigoureusement nul, en le multipliant par l'infini, on obtient l'infini. Et ça par contre, c'est correct.
Merci Raph pour cette précision, mais c'était une démonstration de pataphysique, et je sais pertinemment que la division par 0 est absurde dans la vraie vie. Le jeu de cette démonstration est justement de faire chercher l'erreur au lecteur, c'est bien, tu l'as trouvée, c'est pas une raison pour s'insurger de la sorte…
Tu aurais pu souligner que j'ai effectué plusieurs divisions par 0 aussi:
“b=0
Par conséquent
1=b/b=0”
Je n'aurais pas ajouté le ”(ou pas)” à la fin de ma démonstration si je l'avais prise au sérieux.
D'autre part, je peux te certifier que quand tu prends un vrai 0 de chez 0, tu trouveras 0*infini=0. Au lycée tu as probablement appris que “quelque chose qui tend vers 0” multiplié par “quelque chose qui tend vers l'infini” donne une forme indéterminée, ça c'est le calcul de limites.
Au lycée, tu as aussi un chapitre sur l'intégration avec des règles simple sur l'algèbre de l'intégration.
On a int(constante*f(x)dx) = constante * int(f(x)dx) quelque soit le domaine…
Prenons int(0dx), par définition ça vaut 0: l'intégrale c'est défini pour une fonction >=0 comme la surface entre l'axe des abscisses, la courbe de la fonction et les droites d'équation x=borne, et comme les deux délimiteurs sont confondus ça fait une surface nulle.
A présent appliquons notre petite règle sus-citée:
int(0dx) = 0* int(dx) = 0 * [x]^+infini_-infini (notation LaTeX)
int(0dx) = 0*(+infini—infini) = 0*infini
Ô miracle, on a un vrai infini d'un côté et un vrai 0 de l'autre, et on tombe sur 0…
“En pratique, ce type d’équation ne veut pas dire grand chose” => En es-tu sûr? Si tu parles de vie courante, ça n'est pas plus inutile que le théorème de Thalès. Si tu parles des mathématiciens, ce genre d'équation est plus utile que tu ne le penses: dans la simplification de problèmes ou de formules, pour définir des propriétés qui deviennent intéressantes sur certains champs d'application, etc.
Merci Raph pour cette précision, mais c’était une démonstration de pataphysique, et je sais pertinemment que la division par 0 est absurde dans la vraie vie. Le jeu de cette démonstration est justement de faire chercher l’erreur au lecteur, c’est bien, tu l’as trouvée, c’est pas une raison pour s’insurger de la sorte…
Il ne faut pas te sentir remis en question à la moindre opposition: je ne critique pas tes capacités en maths (enfin pas à ce niveau là), je dis simplement que je n'aime pas ce type de démonstration, qui sont des erreurs grossières maquillées de pseudo raisonnement, pour aboutir à un résultat foireux. L'utilité est donc des plus réduite. Je suis plus séduit par un raisonnement qui se tient, aboutissant à un résultat intéressant. Les réflexions que ces derniers peuvent induire sont à mon sens bien plus constructives.
Là ou par contre j'émets un doute quant à tes compétences en maths, c'est quand tu t'obstines à affirmer 0*infini=0, sans comprendre que le signe infini a été défini pour des raison pratique en analyse, de façon à rendre le corps des réels complets, mais ne peut décemment pas être manipulé comme n'importe quel réel.
Dans ta démonstration tu fais usage d'intégrale non intégrable, qui n'ont par définition aucun sens. A partir de là, il est aisé de leur faire dire ce que bon te semble.
int(0dx) = 0* int(dx) = 0 * [x]^+infini_-infini (notation LaTeX)
Ton intégrale n'est pas définie, elle ne vaut donc pas plus l'infini qu'autre chose. (c'est un autre des problèmes classiquement soumis aux élèves: comprendre qu'à partir d'une hypothèse ne serait-ce que légèrement fausse, on peut aboutir à n'importe quoi)
L'infini est un élément utile à définir pour l'analyse, justement dans le cas des bornes d'intégration. On se place ainsi sur l'ensemble des réels auquel on adjoint deux éléments supplémentaires, + et – l'infini. Ce ne sont pas des nombres. Et le résultats des opérations sont définis de façon à ce que les opérations classiques restent généralement valables.
http://fr.wikipedia.org/wiki/Droite_r%C3%A9elle_achev%C3%A9e#Op.C3.A9rations_ind.C3.A9termin.C3.A9es
Si tu parles des mathématiciens, ce genre d’équation est plus utile que tu ne le penses: dans la simplification de problèmes ou de formules, pour définir des propriétés qui deviennent intéressantes sur certains champs d’application, etc.
Je suis curieux de savoir où tu as trouvé quelqu'un ayant utilisé cette définition des éléments infinis. Si tu as un article, ou n'importe quelle publication en faisant état, je suis preneur.
c'est très intéressant tout ça mais si les pataphysiciens connaissaient le sens du signe =, ils auraient peut être utiliser le ≈, et là, ils auraient eut tout mon agrément pour démontrer toutes leurs inepties ^^
dans le math ainsi que ttes les autres sciences tout est relatif, si on ajoute à ceci que l'homme est un être borné par l'espace; ALORS comment pourra un borné utiliser une composante relative pour mesurer l'Absolu: DIEU.
Heu…. Zetes sur qu'on peut pas calculer le volume d'un pet avec la pataphysique ?
Parceque j'aimerais bien savoir si un foireux (qui sens normalment tres fort) ou un bucheron (qui sens généralement moins fort mais qui est bien plus bruyant) n'est pas moins éfficace…
Evidement tout ca en prenant en compte si on porte un jean slim ou un jean large (espace entre le tissus humain et le tissu textile) afin de déterminer la vitesse de propagation de l'odeur (enfermée ou pas).
\o/
Pour revenir au sujet, retenons quand même que le dit Dr Faustroll n'est qu'un personnage de roman d'Alfred Jarry, inventeur de la 'pataphysique, et qu'à aucun moment cette “science” ne se veut sérieuse.
Ben, vu comme ça, je préfère LARGEMENT me pencher vers la “vrai” physique….
Après, si des fous veulent s'amuser, je n'y vois aucun inconvénients surtout après la remarque de Fragmentor =)
A MON AVIS la pataphysique n'est là que pour poser des questions et faire émaner des idées originales: ainsi, dans le fait de calculer la surface de Dieu, ce n'est pas la réponse qui importe, mais l'action d'avoir cherché à la calculer, ce qui est absurde en soi! Ça fait parler, ça fait poser des questions, ça divise, ça pose un regard mathématique (ce qui est neuf) sur la métaphysique, et aussi, ça stimule l'originalité. Comme toute réponse est de toute façon absurde, autant inventer soi-même une réponse absurde!
La surface de Dieu ne peut se mesurer qu'avec une équation très complexe contenant des fractions avec des 0 en dénominateur et avec les nombres qu'on appelle les inconnues inconnues.
Tout ça me fait penser au film Pi, qui fait lui aussi le lien entre mathématique et divin: un matheux fou cherche une équation globale de la vie et de toute chose, une équation capable de prédire tous les cycles naturels, et boursiers.
Franchement je pense que vous allez trop loin et qu'il faut recentrer le débat : combien de fois Chuck Norris a-t-il compté jusqu'à l'infini ? Là est la vraie question.
Pardon…
sans me poser en donneur de leçon académicien, je précise à Voan que “après que le collège de pataphysique ait fermé en 1975” contient une erreur: on dit “avant qu'il ait fermé” et “après qu'il a fermé”... c'est juste pour rectifier une faute trop souvent commise, pas de prétention mais c'est comme ceux qui écrivent au futur “je pourrais” au lieu de “je pourrai”, je peux pas m'empêcher de réagir, c'est épidermique !
en ce qui concerne la pataphysique, il existe une correspondance surréaliste entre boris vian et raymond queneau, c'est jubilatoire à lire et ressemble finalement à l'esprit des LSV : le LSV ne serait-il pas le fils caché de la pataphysique ??? (bien que nous, et moi le premier, n'ayons pas tous l'étoffe et l'envergure de Vian ou Queneau…)
Je rejoins tout à fait ton état d'esprit Titou et d'ailleurs, tant que que S(CN) > S(D), la terre continuera de tourner.
avec bien entendu pour les moins réveillé d'entre vous S(CN)= surface de Chuck Norris et S(D) = surface de Dieu
J'aime la pataphysique et j'aime les maths. Or ces deux domaines n'ont rien en commun.
Les maths c'est un moyen superbe pour étudier la réalité (y compris celle qui échappe à nos sens) tandis que la pataphysique est le summum de la recherche sur l'esprit humain en allant le plus loin possible dans l'iréel.
Quant au volume d'un pet… on peut en tout cas le mettre entre deux bornes: 0 et le volume d'un intestin. C'est une première estimation.
En tout cas je soutiens Raph dans sa rigueur mathématique. L'infini n'appartient pas à l'ensemble des nombres naturels ou celui des réels, vous ne pouvez donc pas l'utiliser ainsi.
bon, étant une mortelle très classique….. la surface de Dieu pour moi c'est au cm2…...... donc ça dépasse toute ma logique!! au cathé je n'ai jamais appris la considération de Dieu en surface….... je suis perdue….
1=1
1/3=1/3
1/3=0.333333…
3*(1/3)=3*0.3333333…
1=0.999999999…
**siffle**
@clebab_60 :
Tu n'aurais pas déjà lu ceci ailleurs ?
il y a que moi que ça choque le résonnement de Siddhartha.
reprenons du début
hypothèse :soit deux réels a et b, avec a=b!=0
a²=b²=ab
a²-b²=a²-ab (soit 0=0 étant donner que a=b)
(a+b)(a-b)=a(a-b) soit a-b=0
donc
a+b=a b=0=a si on respecte l’hypothèse de départ hors a et b sont différents de 0 donc on a soit a!=b soit a=b=0, Siddhartha a donc effectuer un raisonnement par l'absurde prouvant que résonner de cette manière n'est pas pertinent
Siddhartha a donc effectuer un raisonnement par l’absurde prouvant que résonner de cette manière n’est pas pertinent
Non. As-tu lu la réponse de Raph à ce sujet ? Elle est pourtant très claire je trouve…
j’avoue que jetai un poil fatiguer et que j'ai juste survoler les réponses loupant par la même la réponse de Raph, et commentant une erreur que même un sixième ne ferait pas (sérieusement comment ai-je put faire 0*(a+b)=(a+b)), veuillez donc m'excuser pour ce commentaire servant plus a démontrer mon incompétence qu'autre chose.
Bien que le sujet date un peu .
Je ne suis pas d'accord avec Raph qui maintient que 0*l'infinie est indéterminé .
Il suffit de prendre la fonction f(x) = 0*g(x) avec g(x)->infinie
f(x) est donc une fonction null
(Preuve si scepticisme :
On peut supposé que g(x) ne s'annule jamais étant donné qu'on n'étudie que pour n'importe quel fonction tendant vers l'infinie
f(x) = 0*g(x)
f(x)/g(x) = 0
f(x) =0
)
on sait donc que f(x) = 0
lim f(x) = 0 * lim g(x) = 0* infinie = 0
le zéro pur et dure fois l'infinie donne bien 0 .
c'est comme dire que 1^(infinie) est indéterminé .
Ce n'est pas indéterminé, cela fait bien 1 mais si on a une fonction qui tend vers 1 alors dans ce cas c'est indéterminé .
zokoban : Tu ne peux pas “faire disparaître” g(x) d'une division si g(x)->infini.
Relis les commentaires de Raph. Notamment les notions de différence entre calculs de limite et calculs réels, et celles qui expliquent que l'infini ne doit pas être manipulé comme un réel quelconque.
Le docteur Faustroll et Chuck n'ont rien inventé, les hébreux y avaient déjà pensés ! ;)
- That His height, from His Seat of Glory and up (is) 118 ten thousands
parasangs (rebaboth),
– From His Seat of Glory down (is) 118 ten thousands parasangs (rebaboth),
– His total height 236 ten thousand thousands parasangs.
– From His Right Arm to His Left Arm (is) 77 ten thousand (parasangs).
– From His Right Eye to (His) Left Eye (is) 30 ten thousands (parasangs).
– The Skull on His Head (is) three and one third ten thousand (parasangs).
– The Crowns on His Head (amount to) 60 ten thousands (parasangs) equaling the 60 ten thousands of the tribes of Israel.
Therefore is He called the Great, the Mighty and the Awesome El : KLYTYH YDYDVT EL CHY KLTA 'AVVTA HMQVQ TQTF HQTF HQTM QTF B'ABVR MSVS
“Blessed be the Name of the Glory of His Kingdom for ever.”
PS. Une bière à celui qui me prononce : KLYTYH YDYDVT EL CHY KLTA 'AVVTA HMQVQ TQTF HQTF HQTM QTF B'ABVR MSVS !
http://en.wikipedia.org/wiki/Shi'ur_Qomah
http://www.workofthechariot.com/TextFiles/Translations-ShirQoma.html

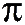



Donc si je comprends bien, il y a un quelqu'un qui a essayer de calculer la surface de Dieu ! Déjà rien que de penser à le faire c'est balèze…
Comme on dit, un con qui marche va plus loin qu'un intellectuel assis !