Vous connaissez peut être cette histoire : sur un échiquier, on place un grain de riz sur la première case, deux grains sur la seconde case, quatre sur la troisième, puis on continue de doubler les grains de riz sur chaque case jusqu’à ce que l’échiquier (de 64 cases) soit rempli. Au final, on obtient (264) – 1 = 18.446.744.073.709.551.615 grains de riz !!
Soit la production terrestre des 962 prochaines années ! (chiffres 2000 : production de riz = 600×106 tonnes et pour un grain de riz évalué à 0,06 g). Ou encore, si ces grains de riz étaient mis bout à bout, cela représenterait la distance de la Terre à Alpha du Centaure (l’étoile la plus proche de la Terre après le soleil). Aller… et retour !
Eternum a raison ! En effet le fait de placer un grain de riz sur la 1ère case correspond à 20 et non à 21 ! Ainsi sur la dernière case on ne place pas (264)-1 grains de riz mais bien 2(64–1)=2^63= 9 223 372 036 854 775 808 grains de riz !!!
De plus, si on veut le nombre total de grains de riz, il faudrait faire 20 + 21 + 22 + 23… Je vous laisse faire tout ça !
En espérant que je ne me suis pas planté !
Chapeau bas, mazerty. J'ai pas résisté :
Le total de la suite (2n) + (2n+1) donne donc : 18 446 744 073 709 600 000 grains de riz. En fait dans la légende, il s'agirait de grains de blé (à voir wiki…) mais pour ne pas dénaturer le LSV, prenons des grains de riz à l'estimation :
On a 18 446 744 073 709 600 000 grains X 0.06 g
soit 1 106 804 644 422 570 kg de grains de riz.
A qui le tour pour nous dire combien ça fait de sacs de “x” kg et le nombre d'années de stockage…? lol
Je renvoi ce LSV en modération aux vues des comms d'eternum et mazerty.
Je ne leur met pas encore de bons points pour ne pas effacer les comms tout de suite, mais ça les mérite largement.
Euh, vous craquez completement les mecs : la chiffre du LSV, c'est le total de toutes les cases, et c'est bien, en sommant de 1 a 263, 264-1
http://en.wikipedia.org/wiki/Geometric_progression#Geometric_series
si vous etes allergiques aux formules :
total jusqu'a la premiere case = 21 – 1 = 1.
total jusqu'a la deuxieme case = 2+1 = 3 = 22-1
total jusqu'a la troisieme case = 1 + 2 + 4 = 7 = 23-1
et ainsi de suite.
Ensuite peut etre qu'il n'y a qu'a moi que ca parait evident que “au final”, il s'agit du total des grains. Je crois bien que le deal entre le mage et le roi etait le nombre total des grains.
Lotharius, un peu de serieux dans la moderation. Faut pas croire le premier commentaire qui a compris le truc a l'envers, hein. Ensuite ca a peut etre besoin d'etre clarifie pour bien expliquer qu'il s'agit de la somme.
Ce n'était pas un manque de sérieux, mais plutôt un excès de prudence. Ne voulant pas corriger moi-même un LSV qui me dépasse, je souhaitais le re-soumettre aux plus matheux des modos (qu'il soit valide ou non) pour vérification. 'fin bon, tant mieux si les comms ne sont pas passés inaperçus après leur validation.
j'avais pas compris à l'envers ! Désolé. Mon idée était de faire valoir que la somme maximale atteinte était en case 64. Mal expliqué ! De plus, je reconnais volontiers que faire totalement confiance au tableur était une erreur :
http//mathematiques.ac-paris.fr/portail/jcmc/d.5773/la-legende-de-l-echiquiercourt.
Evidemment que la suite doit être retranché de 1 pour donner la somme exacte, merci à Junk pour son explication vulgarisée.
Je confirme, la LSV est exacte. Désolé, j'avais mal compris, j'ai cru qu'il s'agissait juste de la 64e case et pas du nombre total de grains :S. Merci à Junk pour cette explication (notamment les formules)
encore (et toujours :D) une victoire de junk… en ce qui concerne les LSV matheux (et toujours une bonne vulgarisation !)
Mouais, en l'occurence pour le LSV proba, c'etait une defaite, vu que Mans a decide de le supprimer.
Et avec un damier ? Y'a 100 cases sur un damier !
Ça fait combien de fois la distance Terre-Alpha ? 2^34 fois non ?
Je viens de m'amuser avec des données plus à jour…
Selon le FAO ( http://faostat.fao.org/site/567/DesktopDefault.aspx?PageID=567#ancor ), la production mondiale de blé en 2008 (données les plus récentes) s'éleverait à environ 689.945.712 t.
Selon Wikipédia ( http://fr.wikipedia.org/wiki/Grain_de_bl%C3%A9 ), un grain de blé pèse de 0,03 à 0,05 g. Calculons donc avec un poids “moyen” de 0,04 g.
Sur cette base, 689.945.712.000.000 g / 0,04 g = 1,725×10^16 grains.
Le calcul du nombre de grains de blé reste le même, soit 18.446.744.073.709.551.615 grains.
Nous avons donc 1069,5 ans de production 2008 sur l'échiquier… Je pense pas qu'il supporterait le poids =D
houlala j'en ai mal à la tête!
Mon frère quans il était jeune avait essayé de faire le calcul aves une calculette! Devinez le résultat? Elle a bloqué
Reposons-nous les neurones
L'instituteur au petit Bruno:
« Deux plus deux?
– Cinq.
« Trois fois deux?
– Dix.
« Dix divisé par deux?
– Un.
« Mais tu ne sais pas compter? Tu me copieras cinquante fois, je suis un âne je ne sais pas compter. »
Le lendemain le petit Bruno revient avec sa punition et la tend au maître:
« Mais tu te fous de moi, tu n'as copié que cinq fois la phrase!
– Mais m'sieur, ce n'est pas ma faute je ne sais compter!
De toute façon tout ces grains ne tiendraient pas sur un échiquier…
[] <——c'est la bas?
Celui qui poste l'anecdote a raison, si on considère le nombre de grain de riz sur une case quelconque, on peut modéliser ce nombre par la suite géométrique de raison 2 et de premier terme 1
Soit U1=1 et Un+1=2Un
n correspond au numéro de la case sur l'échiquier et Un correspond au nombre de grains de riz sur cette case.
La somme de tous les termes consécutifs pour une suite géométrique est:
S= (premier terme)x[(raison)^(nombre de termes)-1]/(raison -1)
Donc si on remplace:
S=1x[(2^64)-1]/(2–1)
=(2^64)-1
C'est juste une impression ou Titi33140 nous réexplique le LSV déjà expliqué, mais avec le mode “prof de maths chiant” sur on ?

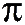


Y'a comme un problème. En effet, le “mage” Sissa proposa le réglement de son travail à son roi selon cette méthode. Mais si on prend le calcul proposé comme exact, il aurait été récompensé par le total de la 65ème case. Or, le résultat de la case 64 est de la moitié de la case 65, donc la base de calcul n'est plus (264)- 1 mais 2(64–1) soit 9 223 372 036 854 775 808. Je sors, maintenant, non ?